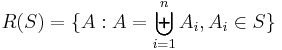Carathéodory's extension theorem

See also Carathéodory's theorem for other meanings.

In measure theory, Carathéodory's extension theorem (named after the Greek mathematician Constantin Carathéodory) states that any σ-finite measure defined on a given ring R of subsets of a given set Ω can be uniquely extended to the σ-algebra generated by R. Consequently, any measure on a space containing all intervals of real numbers can be extended to the Borel algebra of the set of real numbers. This is an extremely powerful result of measure theory, and proves for example the existence of the Lebesgue measure.

1 Semi-ring and ring
2 Statement of the theorem
3 See also
4 References

Semi-ring and ring

Definitions

For a given set Ω, we may define a semi-ring as a subset S of 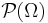$\mathcal{P}(\Omega)$ , the power set of Ω, which has the following properties:

∅ ∈ S
For all A, B ∈ S, we have A∩B ∈ S (closed under pairwise intersections)
For all A, B ∈ S, there exist disjoint sets K_i ∈ S, with i = 1, 2, …, n, such that 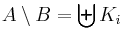$A\setminus B = \biguplus K_i$ (relative complements can be written as finite disjoint unions).

With the same notation, we define a ring R as a subset of the power set of Ω which has the following properties:

∅ ∈ R
For all A, B ∈ R, we have A∪B ∈ R (closed under pairwise unions)
For all A, B ∈ R, we have A\B ∈ R (closed under relative complements).

Thus any ring on Ω is also a semi-ring.

Sometimes, the following constraint is added in the measure theory context:

Ω is the disjoint union of a countable family of sets in S.

Properties

Arbitrary (possibly uncountable) intersections of rings on Ω are still rings on Ω.
If A is a non-empty subset of 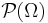$\mathcal{P}(\Omega)$ , then we define the ring generated by A (noted R(A)) as the smallest ring containing A. It is straightfoward to see that the ring generated by A is equivalent to the intersection of all rings containing A.
For a semi-ring S, the set containing all finite disjoint union of sets of S is the ring generated by S:

$R(S) = \{ A: A = \biguplus_{i=1}^{n}{A_i}, A_i \in S \}$

(R(S) is simply the set containing all finite unions of sets in S).

A content μ defined on a semi-ring S can be extended on the ring generated by S. Such an extension is unique. The extended content can be written:

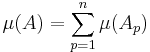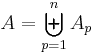$\mu(A) = \sum_{p=1}^{n}{\mu(A_p)}$ for $A = \biguplus_{p=1}^{n}{A_p}$ , with the A_p in S.

In addition, it can be proved that μ is a pre-measure if and only if the extended content is also a pre-measure, and that any pre-measure on R(S) that extends the pre-measure on S is necessarily of this form.

Motivation

In measure theory, we are not interested in semi-rings and rings themselves, but rather in σ-algebras generated by them. The idea is that it is possible to build a pre-measure on a semi-ring S (for example Stieltjes measures), which can then be extended to a pre-measure on R(S), which can finally be extended to a measure on a σ-algebra through Caratheodory's extension theorem. As σ-algebras generated by semi rings and rings are the same, the difference does not really matter (in the measure theory context at least). Actually, the Carathéodory's extension theorem can be slightly generalized by replacing ring by semi-ring.

The definition of semi-ring may seem a bit convoluted, but the following example shows why it is useful.

Example

Think about the subset of 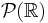$\mathcal{P}(\Bbb{R})$ defined by the set of all half-open intervals [a, b) for a and b reals. This is a semi-ring, but not a ring. Stieltjes measures are defined on intervals; the countable additivity on the semi ring is not too difficult to prove because we only consider countable unions of intervals which are intervals themselves. Proving it for arbitrary countably union of intervals is proved using Caratheodory's theorem.

Statement of the theorem

Let R be a ring on Ω and μ: R → [0, + ∞] be a pre-measure on a R.

The Carathéodory's extension theorem states that^[1] there exists a measure μ′: σ(R) → [0, + ∞] such that μ′ is an extension of μ. (That is, μ′ |_R = μ).

Here σ(R) is the σ-algebra generated by R.

If μ is σ-finite then the extension μ′ is unique (and also σ-finite)^[2].

References

^ Vaillant, Theorem 4
^ Ash, p19

Noel Vaillant, Caratheodory's Extension, on probability.net. A clear demonstration of the theorem through exercises.
Robert B. Ash (1999). Probability and Measure theory. Academic Press; 2 edition. ISBN 0120652021.